Compound Interest

This formula calculates the amount of interest earned on an account or investment where the amount earned is reinvested.

By reinvesting the amount earned, an investment will earn money based on the effect of compounding.

Compounding is the effect of earning interest on the interest that was previously earned.


Calculate

Initial balance (P):
.00
rate (r):
frequency (n):
time (t):

Report



Math Equation Used

Simple Interest Formula:
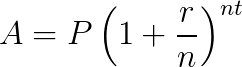
loanFormulaM
where
         A = the new principal sum
         P = the original principal sum
         r = nominal annual interest rate
         n = compounding frequency
         t = the overall length of time the interest is applied (expressed using the same time units as r, usually years).

Example 1 from Wikipedia (see Ref.)
Suppose a principal amount of $1,500 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly.
Then the balance after 6 years is found by using the formula above, with P = 1500, r = 0.043 (4.3%), n = 4, and t = 6:

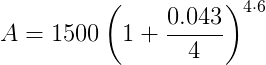
         loanFormulaM

So the new principal A after 6 years is approximately $1,938.84.
Subtracting the original principal from this amount gives the amount of interest received:
         1938.84 - 1500 = 438.84

Example 2
Suppose the same amount of $1,500 is compounded biennially (every 2 years).
Then the balance after 6 years is found by using the formula above, with P = 1500, r = 0.043 (4.3%), n = 1/2 (the interest is compounded every two years), and t = 6 :

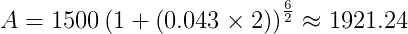
         loanFormulaM

So, the balance after 6 years is approximately $1,921.24.
The amount of interest received can be calculated by subtracting the principal from this amount.
         1921.24 - 1500 = 421.24
The interest is less compared with the previous case, as a result of the lower compounding frequency.

References
Compound interest. (2019, February 11). Retrieved from https://en.wikipedia.org/wiki/Compound_interest